قانون Zipf والقولون. إنه يربط الألعاب بكل شيء وكل شيء للألعاب

المحتوى

• وأوضح قانون Zipf ل
• التجربة الأساسية
• قانون Zipf في أسواق Steam
• ما الذي يمكن أن نتعلمه عن Steam؟
• الاستنتاجات

منذ فترة قصيرة اقترح أحد أصدقائي أن أشاهد فيديو Vsauces على قانون Zipf ومبدأ Pareto ومظاهرهم الغامضة في كل مكان حولنا. إليك دعابة صغيرة لتلفت انتباهك - 80٪ من الناس يعيشون في 20٪ من المدن الأكثر شعبية ؛ 80 ٪ من مجموع الأراضي ينتمي إلى 20 ٪ من أغنى الملاك ؛ 80٪ من إجمالي النفايات موجودة في أعلى 20٪ من الشوارع التي يتم التخلص منها - كما هو متوقع وفقًا لقانون Zipf ومبدأ Paretos.

ليس كافي؟ حسنًا ، كما اكتشفت بالأمس ، فإن ثقب الأرانب لا يتوقف عند هذا الحد ... مليئًا بالشك ، قررت النظر في مقدار الوقت الذي يقضيه الناس في لعب ألعاب Steam ... حسنًا. يتم قضاء 80 ٪ من وقت الناس في لعب 20 ٪ من الألعاب الأكثر شعبية ... ممتع؟ حسنًا ، اقرأ ، هناك المزيد لهذه القصة.

يعد تسجيل Vsauces رائعًا على مدار 20 دقيقة ، وهو يفسر الكثير من الصور الكبيرة عن Zipf ، ومع ذلك فهو خجول جدًا في عرضنا على الآلية الأساسية التي يُعتقد على نطاق واسع أنها تسهم في السبب وراء عمل Zipf. لذلك قبل أن نمضي قدما ، أود أن أوضح ذلك بإيجاز.

وأوضح قانون Zipf ل

هناك عدة طرق مفاهيمية لشرح الحدس وراء مبدأ 20/80. أفضل مثال ، في رأيي ، هو المثال الخاص بحفر القمر.

التجربة الأساسية

لذا ، تخيل لو شئت ، أن هناك قمرًا لم يمس - سطح أملس تمامًا. الآن ، لنفترض أن هناك بعض الكويكبات ذات الحجم العشوائي التي تضرب القمر ويلي. عندما يهبط الكويكب الأول ، فإنه يترك حفرة. الآن واحد آخر يضرب ، وترك حفرة في مكان آخر. كل حفرة هي جزء من إجمالي مساحة السطح ، وبالتالي هناك فرصة أن يضرب الكويكب العشوائي التالي بالقرب من فوهة البركان الحالية وينضم إليها ، مكونًا مجموعة. تتناسب فرصة حدوث كويكب جديد مع فوهة معينة في الحفر مع حجم الكويكبات الموجودة. هذا يعني أن الكويكب العشوائي التالي من المرجح أن ينضم إلى أكبر مجموعة موجودة ، مما يجعله أكبر. نوع من العملية التراكمية ، التي تخلق بعد ذلك آلية غنية بالفقراء تصبح أكثر ثراءً.
ضع ذلك في الاعتبار ، لأنه يُعتقد أنه التفسير العام لـ "لماذا" يعمل قانون Zipfs مع هذه العالمية الغامضة. مثال الكويكب بسيط للغاية ، ولكن السؤال هو ماذا سيحدث خلال العديد من التكرار

محيرة قليلا؟

حسنًا ، لقد قدمت صورة متحركة لدفع هذه النقطة الرئيسية إلى المنزل. NB! سيتم مناقشة الرسم البياني في وقت لاحق ، فقط حاول وتصوير التجربة.

إذا لاحظنا القمر الفعلي ، اتضح أنه مع زيادة كمية الكويكبات إلى كميات كبيرة ، فإن أقطار الحفرة التي تمت ملاحظتها تنمو بحيث تصل نسبة أعلى 20٪ من الحفر الكبيرة إلى 80٪ من مساحة السطح.

لذلك عندما نذهب إلى المزيد من الكويكبات ، فإن توزيع أكثر المجموعات شعبية إلى أقل المجموعات شعبية يقترب من نوع من "التوزيع المثالي" مع هذه الخاصية 20/80 - توزيع Pareto. إذا قمت بالرياضيات ، فقد تبين أنه (بشكل عام) ، إذا كان أكبر مجموعة بالحجم N ، فإن ثاني أكبر مجموعة تكون حول الحجم N / 2 ، والثالثة N / 3 وما إلى ذلك. وهذا ما يسمى قانون Zipf ل. الشيء الغريب هو توزيع قانون Zipf و Pareto يعمل على كمية محيرة من العناصر (الكويكبات) والمجموعات (مجموعات الحفرة). بالطبع ، هناك انحرافات واضطرابات عشوائية ، لكن الاتجاه العام لا يمكن إنكاره.
آمل أن تتمكنوا من رؤية كيف أن الكويكبات التي من المحتمل أن تضرب الحفر الكبيرة على سطح القمر ترتبط بالمدن أكثر جاذبية ، إذا كان هناك بالفعل المزيد من الأشخاص الذين يعيشون فيها. ومع ذلك ، يتعين على المرء أن يدرك أن المدن بعيدة عن "المجموعات" الوحيدة التي تتصرف وفقًا ل Zipf.

فيما يلي بعض الأمثلة من بحث مارك نيومانز عن توزيعات باريتو. NB! الرسوم البيانية في نطاق سجل الدخول الذي يسهل الشكل الزائدي للمنحنيات ، ويقدم علاقة خطية تقريبًا.

الأولي y = aX ^ (- b)
سجلات كلا الجانبين => log y = log a - b log X

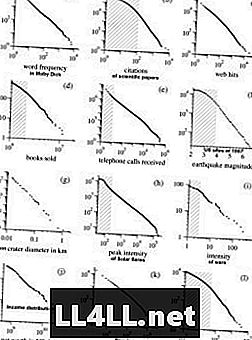
ومن المثير للاهتمام أن هذا الاتجاه هو نفسه الذي تظهره الطوائف الدينية ... والملكية المشتركة لمعظم هذه الظاهرة هي ببساطة ميل "المجموعات الكبيرة - الحصول على أكبر". لذلك فإن قانون Zipf ثابت في الآليات ، حيث ترتبط تفضيلات العناصر إيجابيا بحجم المجموعات (بمعنى أنه كلما كانت المجموعة أكبر ، زاد احتمال نموها). هذا هو السبب في أنني أحب أن أفكر في المجموعات كمجموعات وعناصر كمجموعات.

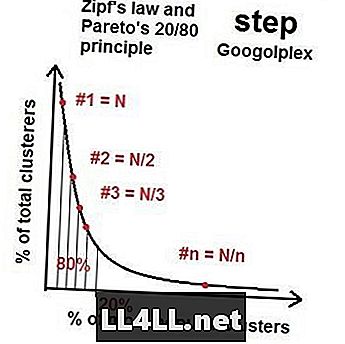
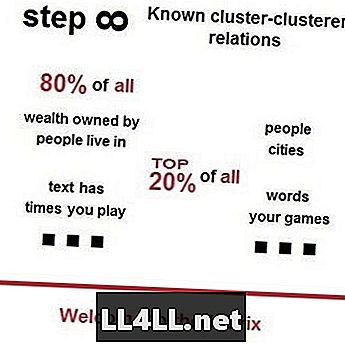
قانون Zipf في أسواق Steam

المشبوهة من هذا الأخير؟ هنا هو مقدار الوقت الذي يقضيه الناس على الألعاب الأكثر شعبية على Steam .. بيانات من SteamSpy.

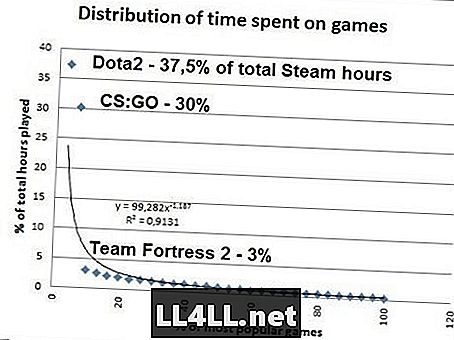
إذا قمت بالرياضيات ، فقد تبيّن أن 20٪ من ألعاب Steam الأكثر شيوعًا تمثل 80٪ من إجمالي كمية اللعب ، لذلك فإن لغز Pareto 20/80 يعمل مثل السحر هنا ... يجب على المرء أن يلاحظ أنه Zipf ليكون صحيحا ، CS: GO يحتاج إلى حساب 37،5 ٪ / 2 = 18،8 ٪ من إجمالي الوقت بدلا من ضخم 30 ٪. ولكن جانبا من هذا غريب (توقف اللعب CS: GO) ، التوزيع مثل Zipf هو واضح هناك.

هنا هي كمية النسخ المباعة للألعاب الأكثر شعبية.

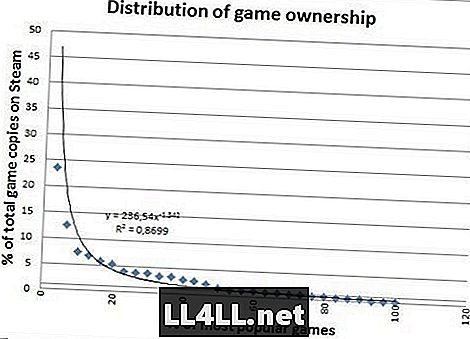
يبدو أجمل بكثير إيه؟ لا تحتوي النسخ المباعة على قيم كبيرة ، لذا فهي مناسبة بشكل جيد للغاية ، وهذا فرق مهم. ومع ذلك ، هناك شيء أكثر إثارة للاهتمام نستنتجه من الاختلافات في الرسوم البيانية الأخيرين.
هل تلاحظ كيف أن "الذيل" الذي يذهب إلى اليمين هو نوع من الدهون في الرسم البياني الثاني؟ حسنًا ، بعبارات بسيطة ، يخبرنا ذلك أن الألعاب "غير المحبوبة نسبيًا" تحظى بشعبية كبيرة مقارنةً بالمؤامرة السابقة.
في الواقع ، اتضح أن 20 ٪ من الألعاب الأكثر شعبية تمثل 60 ٪ فقط من المبيعات ، مقابل 80 ٪ من اللعب. مثير للإعجاب؟ تراهن مؤخرتك هو عليه.

ما الذي يمكن أن نتعلمه عن Steam؟

حسنًا ، إن حقيقة أن شعبية اللعبة تتبع توزيع Pareto تخبرنا أنه يوجد بالفعل نوع من التأثير الإيجابي على الشبكة ، مما يجعل اللاعبين يختارون الألعاب التي يلعبها بالفعل المزيد من الأشخاص. ما يخبرنا به الفرق في سمنة ذيول هو أن مستخدمي Steam أصبحوا أكثر "عمياءً عن حجم المجموعة" ، عند شراء الألعاب أكثر منهم عند لعبها.
فكر في الأمر - فكلما زاد عدد الأشخاص الذين يشترون الألعاب بصرف النظر عن "الرأي العام الحالي" ، زاد توزيع Pareto بالارض ، لأنه من غير المرجح أن تنمو الألعاب الكبيرة بدرجة أكبر. إذا لم يعط أحد جرذانًا بشأن عدد الأشخاص الذين يلعبون بالفعل لعبة وكان توفر جميع الألعاب هو نفسه ، فإننا نتوقع أن تمثل 20 ٪ من الألعاب الأكثر شعبية حوالي 50 ٪ من المبيعات ووقت اللعب (على سبيل المثال ، افتراض أن التفضيلات الفردية هي موزع طبيعيا).

الاستنتاجات

لذلك هناك عاملان يساهمان في توزيع Pareto في أسواق Steam - مدى ابتكار المطورين (عدد حفر القمر الجديدة التي يتم تشكيلها) ومقدار اللاعبين (الكويكبات) قيمة المجموعة الحالية ، عند اختيار المجموعة المراد الانضمام إليها . كما اتضح ، فإن اللاعبين يشعرون بالحجم الكبير للمجموعات عند شراء الألعاب ، ولكن العكس هو الصحيح عندما يلعبون بها. رائع. صحيح؟

إذا كنت تريد معرفة المزيد عن توزيعات قانون وقانون Zipf ، فهناك محاضرة لطيفة. علاوة على ذلك ، تأكد من إلقاء نظرة على ورقة نيومان!
إذا كنت ترغب في قراءة المزيد من هذا النوع من الأشياء ، فسنحاول قريبًا الانضمام إلى هذه الملاحظة في نموذج يوضح أن الألعاب متعددة اللاعبين الأكثر شعبية لها أسعار أعلى (والتي ترتبط بتفضيل اللاعبين للانضمام إلى مجموعات أكبر حجمًا). انظر المقال هنا. سيحاول مقال Piece De Resistance الانضمام إلى هذه النظريات مع توضيح كيف أن الألعاب متعددة اللاعبين والشبكات الاجتماعية والمدن هي في الواقع جميع السلع المعادية للمنافسة مع تأثيرات الشبكة ، (وكلما زاد استهلاك الناس لمزايا جيدة ، زاد عدد مستهلكي كل فرد) يحق لهم مع هذا الضباب Zipfian من الغموض ...

حتى ذلك الحين - استمتعوا بأنفسكم!

ملاحظة بث في تعليق مع فكرة ممتعة لعلاقة 20/80 تعتقد أنه قد يكون صحيحا.

الألغام هي:
80 ٪ من الناس الحنين إلى سببها 20 ٪ من أسعد ذكرياتهم (ثبت فعلا لمعدل ينسى الناس المعلومات في)
80 ٪ من الكتلة تتركز في 20 ٪ من أكبر الأجسام الفضائية (ثبت فعلا لتوزيع قوة الجاذبية)
وبالطبع
80٪ من الفوضى في مرحاضك تأتي من 20٪ مما تأكله (لا توجد أبحاث أكاديمية تتحدث عنها)